Mechanika

Pohyb hmotného bodu

Mechanika je obor fyziky, který se zabývá mechanickým pohybem těles (jejich přemísťováním).

Hmotný bod je fyzikální model používaný při studiu pohybu těles (fyzikálním modelem rozumíme objekt nebo jev, jehož některé reálné vlastnosti prostě pomineme - v případě hmotného bodu zanedbáme například tvar a rozměry popisovaného tělesa, ne však jeho hmotnost).

Pro popis pohybu hmotného bodu je nezbytné mít možnost určit (změřit) jeho polohu. Určení polohy je možné pouze vzhledem k jiným bodům, tělesům - je tedy nutné zvolit pro určení polohy tzv. vztažnou soustavu.

Mění-li se poloha sledovaného hmotného bodu vzhledem ke zvolené vztažné soustavě, říkáme, že se hmotný bod ve vztažné soustavě pohybuje, v opačném případě je v klidu (je zřejmé, že jeden a tentýž hmotný bod může být vzhledem k jedné vztažné soustavě v klidu, zároveň vzhledem k jiné v pohybu - říkáme, že pohyb a klid jsou relativní).

Trajektorie pohybu hmotného bodu

Zaznamenáme-li všechny body v prostoru, kterými hmotný bod při svém pohybu prošel, získáme tzv. trajektorii pohybu (trajektorie = křivka).

Dráha pohybu

Dráhou pohybu hmotného bodu rozumíme délku trajektorie.

Rychlost pohybu

Vydělíme-li dráhu hmotného bodu časem, který byl k jejímu překonání potřeba, získáme veličinu, která se nazývá průměrná rychlost pohybu.

Pokud určujeme průměrnou rychlost pohybu v nějakém krátkém časovém intervalu a případně tento interval dále zkracujeme, blíží se takto určená průměrná rychlost hodnotě, kterou nazýváme okamžitá rychlost pohybu.

Zrychlení

Změnu rychlosti pohybu popisuje veličina zvaná zrychlení.

Důležitá poznámka: Protože rychlost je vektorová veličina, může se měnit nejen její velikost, ale i směr! 

Vydělíme-li změnu rychlosti hmotného bodu časem, který byl k jejímu získání potřeba, získáme veličinu, která se nazývá průměrné zrychlení.

Druhy pohybů

- z hlediska trajektorie:

pohyb přímočarý (trajekorií je část přímky)

pohyb křivočarý

- z hlediska rychlosti:

pohyb rovnoměrný (zrychlení je nulové)

pohyb nerovnoměrný (pohyb zrychlený)

Newtonovy pohybové zákony

Pohybem těles bez ohledu na jejich hmotnost a působící síly se zabývá část mechaniky zvaná kinematika - zabývá se pouze geometrií pohybu.

Závislostí mezi pohybem teles a silami, které na něj působí, se zabývá část mechaniky zvaná dynamika - zkoumá příčiny pohybu.

Základem dymaniky hmotného bodu jsou tzv. Newtonovy pohybové zákony.

1. Newtonův pohybový zákon (zákon setrvačnosti)
Těleso setrvává v klidu nebo v rovnoměrném přímočarém pohybu, dokud není nuceno působením vnějších sil tento stav změnit.

2. Newtonův pohybový zákon (zákon síly)
Zrychlení tělesa je přímo úměrné působící síle a má s ní stejný směr.

3. Newtonův pohybový zákon (zákon vzájemného působení, akce a reakce)
Síly, jimiž na sebe působí dvě tělesa, mají vždy stejnou velikost a opačný směr.

Práce a energie

Mechanická práce W vyjadřuje dráhový účinek síly působící na těleso.

Mechanickou práci koná pouze síla, která působí ve směru pohybu tělesa (síla, která působí kolmo ke směru pohybu nebo která nepohne tělesem, práci nekoná).

Působí-li síla F na těleso pohybující se po dráze s, pak vykoná práci

W = F . s . cos,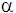

kde 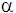 je úhel, který svírá vektor síly F se směrem pohybu tělesa.

Jednotkou mechanické práce je N.m, pro tuto důležitou jednotku je zavedeno označení J (joule).

Vykoná-li síla práci (např. při uvedení tělesa do pohybu, vyzvednutí tělesa do výšky, roztočení tělesa kolem osy, ...) a přestane na těleso působit, zůstává vykonaná práce v tělese přítomna ve formě, kterou nazýváme mechanická energie.

Rozlišujeme dva druhy mechanické energie

- pohybovou (kinetickou) E_k - je spojena s pohybem tělesa

- polohovou (potenciální) E_p - je spojena s polohou tělesa v gravitačním, elektrickém, magnetickém poli nebo s pružnou deformací tělesa (natažená pružina, nafouknutý míč)  

Při mechanických dějích přechází pohybová energie v polohovou a naopak, jejich celkový součet se při nich nemění = zákon zachování mechanické energie:

E = E_k + E_p = konst.

Výpočet kinetické energie tělesa s hmotností m, které se pohybuje ve zvolené vztažné souustavě rychlostí v: 

E_k = (1/2).m.v²

Výpočet potenciální energie tělesa s hmotností m, které bylo ve stejnorodém gravitačním poli s tíhovým zrychlením g zdvihnuto do výšky h: 

E_p = m.g.h

Jednotkou energie je J (joule).

Mechanika tuhého tělesa

Zkoumáme-li působení sil na tělesa a nikoli pouze na hmotné body, je situace mnohem zajímavější. Přitom tělesem budeme rozumět hmotný objekt, který se působením vnějších sil nedeformuje (bývá označován jako tuhé těleso).

Síla, která na těleso působí, může přivodit jeho posunutí nebo otočení.

Posuvný účinek síly se neliší od působení na hmotný bod, otáčivý účinek síly si však zaslouží bližší zkoumání. 

Představme si těleso otáčivé kolem pevné osy (působící síla nemůže těleso posunout, pouze otočit kolem osy). Je zřejmé, že síly stejné velikosti ale různých směrů a působišť budou mít na těleso různé otáčivé účinky (vyzkoušejte např. s pootevřenými dveřmi, jejichž osu otáčení určují panty) - některá síla s dveřmi pohne snadno, některá tíž a některé síly s nimi nepohnou vůbec - jaké pravidlo platí pro velikost otáčivého účinku síly?). 

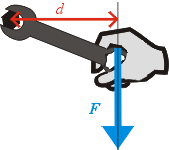
Otáčivý účinek síly charakterizuje vektorová veličina moment síly M = F.d, její jednotkou je Nm.

Podobně jako síly můžeme skládat i momenty sil působící na těleso otáčivé kolem pevné osy - je-li součet momentů různých sil působících na těleso nulový, říkáme, že jsou působící síly v rovnováze.

Zvláštním případem působení sil na tuhé těleso je tzv. rovnováha tuhého tělesa - působící síly nezpůsobí změnu jeho pohybového stavu. 

Rozlišujeme tyto druhy rovnovážného stavu tělesa:

Stálou (stabilní) rovnovážnou polohu - má těleso, které se po vychýlení samovolně vrací zpět do rovnovážné polohy:

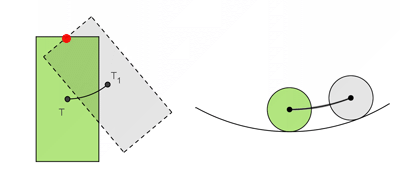
Vratkou (labilní) rovnovážnou polohu - má těleso, u kterého se po vychýlení z rovnovážné polohy výchylka zvětšuje a těleso se samo do rovnovážné polohy nevrátí:

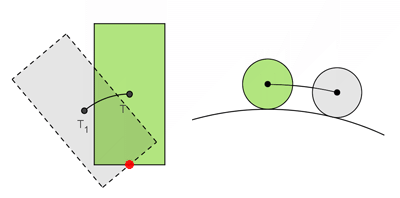
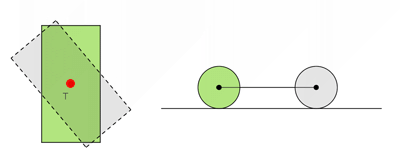
Volnou (indiferentní) rovnovážnou polohu - má těleso zavěšené ve zvláštním bodě, který nazýváme těžiště tělesa - po vychýlení z rovnovážné polohy zůstává v nové poloze, výchylka se nemění - těleso je opět v rovnovážné poloze:

Mechanika kapalin

Pojem tekutina je společný název pro plyny a kapaliny (popř. plazmu). 

V tekutinách na rozdíl od pevných látek nejsou částice vázány na jedno místo, mohou se relativně volně pohybovat.

Protože zkoumání reálných tekutin je příliš komplikované, používáme pro popis jejich chování modely - ideální plyn, ideální kapalinu.

Ideální plyn - dokonale stlačitelný a jeho částice na sebe nepůsobí přitažlivými silami.

Ideální kapalina - dokonale nestlačitelná a její částice na sebe nepůsobí přitažlivými silami (teče bez vnitřního odporu, viskozity)

Pro předpovídání chování kapalin v klidu nám slouží zákony hydrostatiky, pro předpovídání chování proudících kapalin zákony hydrodynamiky.

Hydrostatika

Pascalův zákon
Tlak vyvolaný působením vnější síly na povrch kapaliny se projeví stejnou změnou ve všech místech kapaliny a nezávisí na směru působící vnější síly.

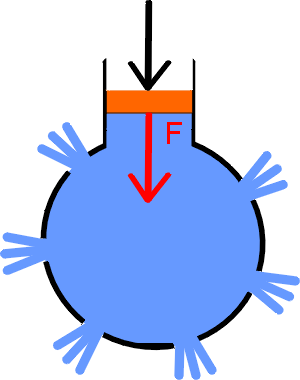
Platí Pascalův zákon v plynech? 
Jak Pascalův zákon v praxi využíváme?

Archimedův zákon
Na těleso ponořené do kapaliny působí vztlaková síla, která je stejně veliká jako tíha kapaliny tělesem vytlačené.

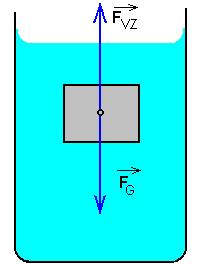
Platí Archimedův zákon i pro plyny?
Uveďte příklad užití Archimedova zákona.